Reverse Mortgage Calculators Explained

Details

Category: Reverse Mortgage Calculators Explained

In this article, we compare the numeric output of an amortization schedule for an amortizing mortgage to a reverse amortization schedule for a reverse mortgage. The loan balances of these two types of mortgages go in opposite directions. The amortizing mortgage outstanding loan balance amortizes, and the reverse mortgage outstanding loan balance accretes.

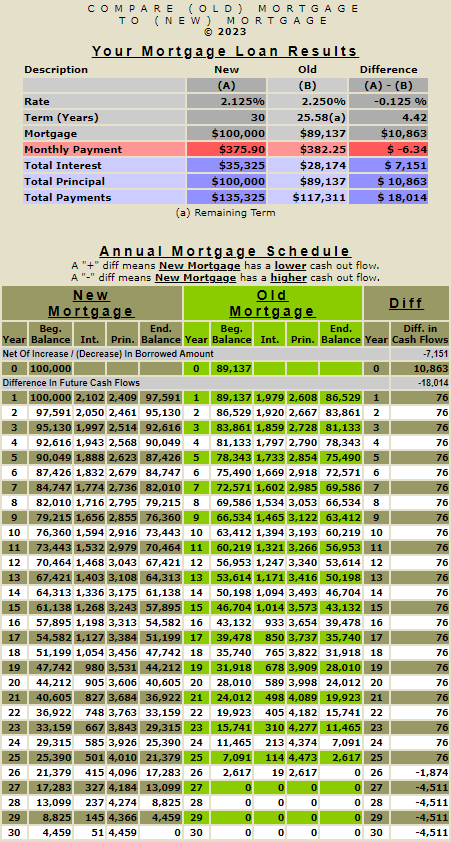
Let's look at refinancing a $100,000 fixed-rate 7% amortizing mortgage into a reverse HECM mortgage with an expected rate of 7%. Immediately below is the monthly payment on a 7% 30-year fixed-rate mortgage, $665.30. Refinancing this loan into a HECM mortgage with an expected rate of 7% will eliminate the need to make monthly mortgage payments on the fixed-rate 7% amortizing mortgage. 

Here is the 30-year amortization schedule for the fixed rate 30-year $100,000 at 7% amortizing mortgage.

Refinancing the fixed rate 30-year 7% amortizing $100,000 mortgage into a HECM reverse mortgage with an expected rate of 7% will incur an upfront MIP (Mortgage Insurance Premium) cost. This upfront MIP, which is a one-time fee, is calculated based on a home's appraised value up to the maximum claim amount of $1,149,850.  The upfront MIP in this example is $ 8,843 or (2% x $442,149). This is in addition to other estimated closing costs of $4,789 (1.08316% x $442,149), resulting in a total of financed closing costs of $13,632 ($8,843 + $4,789).

Hence, on day 1, the original fixed rate amortizing mortgage of $100,000 converted into a HECM reverse mortgage is now $113,632. The upfront MIP of 2% is applied to the home's appraised value unless the appraised value is above the maximum claim amount of $1,149,850. In addition, a HECM reverse mortgage charges an ongoing MIP of .50 percent (50 basis points).

Here, they are side by side below. On the left is the amortization schedule for an amortizing 7% fixed rate mortgage, and on the right is a HECM FHA 7% reverse amortization schedule. As you can see, the starting balance of the 7% fixed rate amortizing mortgage is $100,000, and the starting balance for the HECM FHA 7% reverse amortizing mortgage is $113,632 ($100,000 plus closing costs of $13,632).  The interest and the ongoing MIP are added to the HECM FHA mortgage annually, and the outstanding balance grows. By the end of 30 years, the 7% fixed rate amortizing mortgage is 0, and the balance of the HECM FHA 7% reverse amortizing mortgage is $1,070,590.

This comparison of the amortization schedule for the 7% fixed rate 30-year mortgage and the HECM FHA 7% reverse mortgage vividly illustrates the compounding effect of money. Both these loans, despite having the same interest rate, lead in different monetary directions. The 7% fixed rate mortgage follows a traditional path of monthly payments, while the HECM FHA reverse mortgage offers the unique benefit of being able to forego making monthly mortgage payments. But for comparative purposes, let’s examine what might happen if we paid the monthly $665.30 payment required on the 7% fixed rate amortizing mortgage towards the HECM FHA reverse mortgage. This monthly payment would equal annual payments of $7,983.60 or ($665.30 x 12 months).  

By the end of 30 years, the 7% fixed rate amortizing mortgage is 0, and the balance of the HECM FHA 7% reverse mortgage is $174,135. The $174,135 reflects the compounding effects in the difference in the starting balances of the two mortgages $13,632 ($113,632 - $100,000) and the additional .50% ongoing MIP. I have approached the above example segmentally to isolate the various mathematical impacts.

So, what are the numerical benefits of getting a reverse mortgage over a typical amortizing mortgage? The answer is liquidity, and it is essential to note that these ending differences in the outstanding balances of these two types of mortgages. will be narrower in a lower interest rate environment. Continue to the next page for further discussion.  

Details

Category: Reverse Mortgage Calculators Explained

This article will examine the effects of interest rate levels and their accumulative effect on a reverse mortgage over time.  

In the previous article, "Comparing an Amortizing Mortgage to a Reverse Mortgage," we viewed the effects of the compounding of money. We compared the numeric differences between an amortizing mortgage versus a reverse amortizing mortgage utilizing a 7% fixed rate and a 7% expected rate, and both these mortgage balances went in different directions. For instance, we found that after 30 years, the amortizing mortgage had reduced the principal by [100%], while the reverse amortizing mortgage had increased the principal by [842%].  The differences were somewhat shocking, and ultimately, one might question the utility of a reverse mortgage.  The answer is in the additional liquidity a reverse mortgage provides and the increased advantages of reverse mortgages in a low-interest rate environment.  

In the previous article, we compared a 30-year 7% fixed rate amortizing mortgage to an HECM FHA reverse mortgage with an expected rate of 7%. As a recap, see the below table. Refinancing the fixed rate 30-year 7% amortizing $100,000 mortgage into a HECM reverse mortgage with an expected rate of 7% will cost $8,843 in upfront MIP plus other estimated closing costs of $4,789 for a total of financed closing costs of $13,632. Hence, on day 1, the original mortgage of $100,000 is now $113,632.

The starting balance of the 7% fixed rate amortizing mortgage is $100,000, and the starting balance for the HECM FHA 7% reverse mortgage is $113,632 ($100,000 plus closing costs of $13,632).  The interest and the ongoing MIP are added to the HECM FHA mortgage annually, and the outstanding balance grows. By the end of 30 years, the 7% fixed rate amortizing mortgage is 0, and the balance of the HECM FHA 7% reverse mortgage is $1,070,590.

Before we delve into the liquidity benefits of a reverse mortgage, let's explore the potential benefits of a lower interest rate environment. This shift to a lower interest rate environment could significantly impact the financial results.  Below is a comparison of similar circumstances, except now, mortgage rates are not 7% but a hypothetical 3%. Remember, reverse mortgages accrete; a higher interest rate will only exemplify the compounding effect on a reverse mortgage's outstanding loan balance over time or vice versa. In the example below, the compounding impacts diminish due to a lower rate of 3%, but the opposite effect would result if the interest rate increased. These analyses assume a constant interest rate over the life of the mortgage.  If a mortgage has an adjustable interest rate, then over time, the results would be subject to future changes in interest rates. 

In the above table, the reverse mortgage with an expected rate of 3% ended year 30 with a loan balance of $385,286, whereas in our previous example, our reverse mortgage with an expected rate of 7% ended year 30 with a loan balance of $1,070,590.

The starting balance on the HECM FHA mortgage with an expected rate of 3% differs from the previous example of 7% because, in this instance, the borrower is due to receive an "initial cash advance" of $21,400 at closing due to a change in the "principal limit factor."  The "initial cash advance" is determined by multiplying the "principal limit factor" by the "initial property value" multiplied by 10%. The "principal limit factor" is based on the "age of the youngest borrower" and the "expected rate." The "initial cash advance" of $21,400 must be added to the opening balance of $113,632. The starting balance represents $100,000 plus the financed closing costs of $13,632 plus the "initial cash advance" of $21,400 for $135,023. I will delve into the "initial cash advance" and the "initial principal factor" in a subsequent article. For now, I am trying to isolate the compounding effects of money on the outstanding balance based on different interest rates.

In addition, by the end of 30 years, the 3% fixed-rate amortizing mortgage will be 0. The balance of the HECM FHA 3% reverse mortgage is now $385,286, including the initial cash advance of $21,400 and any interest and ongoing MIP on this amount. Though we are attempting to focus on the impact of the interest rate environment on reverse mortgages, the initial cash advance has more to do with liquidity. Still, as I previously mentioned, I will address this in a subsequent article.

Now, we can begin to discuss the liquidity benefits, but in doing so, we first need to understand the "principal limit factor" and how it might impact our analysis. 

Details

Category: Reverse Mortgage Calculators Explained

The current article will delve into the liquidity benefits of a reverse mortgage, but to do so, we need to understand how liquidity is tapped from a home's equity by the owner utilizing a reverse mortgage. We need to understand the calculations to know how much equity a HECM reverse mortgage can provide. Please read the previous three articles on reverse mortgages before delving into this section on liquidity.  Here is a list: 

Mathematically, What is a Reverse Mortgage?

This article gives a brief numeric description of a reverse mortgage versus an amortizing mortgage.

Comparing an Amortizing Mortgage to a Reverse Mortgage

This article compares the amortization schedule of an amortizing mortgage to a reverse amortization schedule of a reverse mortgage.

Reverse Mortgages in a Low Interest Rate Environment

This article highlights the effects of interest rate levels on the economics of a reverse mortgage versus an amortizing mortgage.

---

Let's discuss the "principal limit factor" and the "initial principal limit," two variables used to determine a home's equity accessibility via a HECM reverse mortgage.

The "principal limit factor" is used in determining the "initial principal limit," which further drives the "initial cash advance" and the available "line of credit."

The "principal limit factor" is based on the "age of the youngest borrower" and the "expected rate." The "age of the youngest borrower" and the "expected rate" are used to obtain the "principal limit factor" from a table with HUD.  

The "initial principal limit" is based on  the "principal limit factor" multiplied by the "maximum claim amount."  The "maximum claim amount." is the lesser of the "initial property value" or $1,149,850. $1,149,850 is the maximum claim amount available for a HECM FHA reverse mortgage.

In the previous article there was an "initial cash advance" of $21,400 in our 2nd example forwarded to the borrower at closing.  In addition, there is a growing "line of credit", $78,968, at the end of year 1.  

The reason for the "initial cash advance" and the "line of credit" is the change in the "principal limit factor" resulting from a shift in the "expected rate" on the HECM reverse mortgage from 7% to 3%.  

The "principal limit factor" for "age of the youngest borrower" of 55 and the "expected rate" of 3% is .484.

The "principal limit factor" for "age of the youngest borrower" of 55 and the "expected rate" of 7% is .257.

The "initial principal limit" for a property value of $442,149 and a "principal limit factor" of .484 is $214,000 ($442,149 x .484).

The "initial principal limit" for a property value of $442,149 and a "principal limit factor" of .257 is $113,632 ($442,149 x .257).

Here is a flow chart depicting the relationship between "age of the youngest borrower" and "expected rate" with the "principal limit factor" which drives the "initial principal limit".

Now we need to calculate the "net principal limit". The  "net principal limit" is the "initial principal limit" less any "mandatory obligations." The "mandatory obligations" would be any existing liens, the upfront MIP, and the other closing costs.  Below is a flow chart showing how the "net principal limit" is derived.

Now, we need to calculate the "initial advance." The "initial advance" is typically 10% of the "initial principal limit" unless the "net principal limit" is insufficient to allow for the total amount. If the "net principal limit" is less than the "initial advance," the "net principal limit" will supersede the "initial advance" ("initial principal limit" multiplied by 10%), and the "net principal limit" will become the "initial advance."  If the "net principal limit" is not only below the "initial advance" but is negative, then the loan is considered "short to close."

In our original analysis, I set the property appraised value to $442,149, the age of the youngest borrower to 55, and the expected interest rate to 7% so that the "principal limit factor" resulted in a 0 "initial cash advance" and a "loan balance" equal to the "principal limit" so that the "line of credit" would be 0 throughout the life of the mortgage.  The "line of credit" is the difference between the "principal limit" and the "loan amount." 

---

In Summary:

The "net principal limit" will determine the net available liquidity that can be accessed utilizing a reverse mortgage. 

Use the below to determine the "principal limit factor" from the HUD tables.

• "age of the youngest borrower"
• "expected rate"

Take the "principal limit factor" multiplied by the "maximum claim amount." (derived from the lessor of the "initial property value" or $1,149,850) to determine the below:

• "initial principal limit"

Subtract the "mandatory obligations" (upfront MIP, other closing costs, and outstanding liens) from the "initial principal limit" to determine the below:

• "net principal limit"

If the "net principal limit" is above the "initial advance," there is liquidity. If it is below the "initial advance" but still positive, there is some liquidity. If it is negative, the loan is "short to close," and there is no additional liquidity.

Note: If you want to run some calculations by changing the input, try this calculator, HECM Reverse Mortgage LOC Calculator. This calculator will automatically obtain the "principal limit factor" based on the "age of the youngest borrower" and the "expected rate." It will run all the calculations based on the required input, "age of the youngest borrower," "expected rate," "initial property value," and "liens payoff."  It is best not to change the input for "MIP (Upfront Mortgage Ins.)" = 2%, "MIP (Ongoing Mortgage Ins.)" = .50%, and "Expected Appreciation" = 4%. These are relatively fixed.