A Step By Step Approach To Using These Mortgage Calculators

Introduction

This section will take you through a step-by-step explanation of how a mortgage calculator works and how to interpret the results. This approach is intended to start with a basic mortgage calculator and then build up to more complex calculators. 

Step 1: Calculating An Amortization Schedule

Your standard mortgage calculator usually calculates your monthly payment based on your anticipated mortgage's 1) balance, 2) term, and 3) fixed rate. Some (like the one we are about to try) will also display an amortization schedule of the loan, separating the annual principal and interest. Now click here for Basic Mortgage Calculator (Single Loan) and enter the required information to obtain the results.

Step 2: Comparing Two New Loans w/o Early Payoff

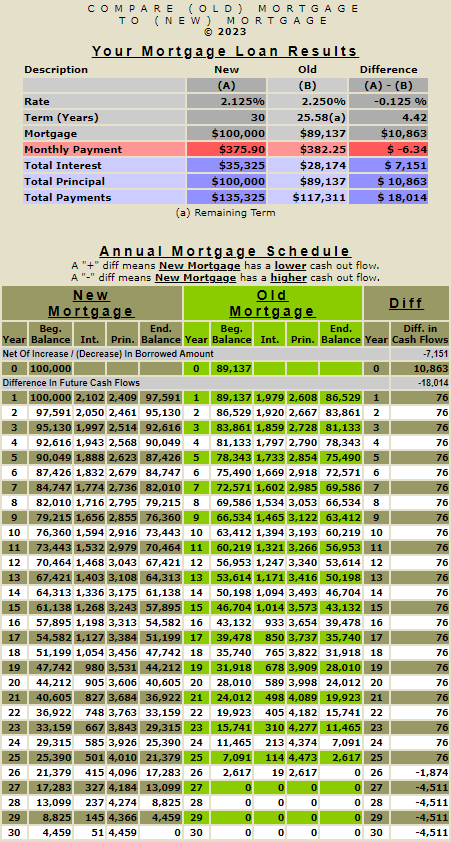
Let us compare two amortizing loans with all the same terms except the interest rate. Click here to Compare 2 New Loans w/o Early Payoff. The default balances for both loans are $100,000. The default term for both loans is 30 years. The default rate for loan #1 is 2.125%, and the default rate for loan #2 is 2.250%. Generating the results will show:

1. A difference in the rates of 0.125%.
2. A difference in the monthly payment of $6.34.
3. A difference in total interest payments over the life of the two loans of $2,284.
4. A difference in total payments (principal & interest) over the life of the two loans of $2,284.

Since the initial principal on both loans is $100,000, the $2,284 difference in cash flows over the life of the loan is all interest. If you refinance to the lower rate, you will save $2,284 in interest (assuming you hold the loan to maturity).  

This is a great little analysis. It is 1) clean, 2) straightforward, and 3) easy to interpret. 

However, there are some limitations to this type of simple mortgage calculator, i.e., 1) no ability to adjust for early payoff of the loan, 2) no ability to adjust for a loan that may have already begun amortizing, and 3) no ability to adjust for the effects of present value and the time value of money. 

What happens if you decide to stay in the home for only 8 years instead of 30 years. What is the benefit in interest savings. The next example will use the same two loan comparison except assume that you will sell the home after 8 years and pay off the new loan.

Step 3: Comparing Two New Loans w/ Early Payoff

Let us now compare two amortizing loans with all the same terms except the interest rate, and also let us anticipate that we will sell the property in 8 years and pay off the loan early. Now click here to Compare 2 New Loans w/ Early Payoff. The default term for both loans is 30 years. 

The default rate for loan #1  is 2.125%, and the default rate for loan #2 is 2.250%. The default value for "How Long Do You Expect To Live In The Home?" is 30; however, change this to 8. Generating the results will then show:

1. A difference in the rates of 0.125%.
2. A difference in the monthly payment of $6.34.
3. There is a difference in total interest payments over the life of the two loans of $931.
4. A difference in total payments (principal & interest) over the life of the two loans of $931.

Hence, instead of saving $2,284 in interest, you will only benefit from saving $931 by refinancing to the lower rate.

However, there are still some limitations to this simple mortgage calculator, i.e., 1) no ability to adjust for a loan that may have already begun amortizing, and 2) no ability to adjust for the effects of present value and the time value of money. 

It gets better. Let's say your existing loan has a balance of $89,137, and you want to refinance with a new loan of $100,000, thereby taking about $10,863 out of your home equity.  What will that look like? Continue to the following example.

Step 4: Comparing An Old Loan To A New Loan

Let us compare two 30-year amortizing fixed-rate loans, old and new. The new loan will have a principal balance of $100,000. We will assume the old loan (the current existing loan on the property) was originally $102,000, has been amortizing for several years, and has a remaining principal balance of $89,137. Now click here to Compare (Old) Mortgage To (New). The default term for both loans is 30 years. The default rate for the new loan is 2.125%, and the default rate for the old one is 2.250%. The default value for "How Long Do You Expect To Live In The Home?" is 30. Leave this at 30 for now. 

Now, generating the results will show the following:

1. A difference in the rates of 0.125%.
2. A difference in the monthly payment of -$13.99.
3. There is a difference in total interest payments over the life of the two loans of $7,952.
4. A difference in total payments (principal & interest) over the life of the two loans of $18,815.
5. The difference in the loan terms is 5.08 years. 

This is a great little analysis. Unfortunately, it is relatively 1) clean, but 2) not so straightforward, and 3) not so easy to interpret. Though the loan rate is lower by .125%, the additional $10,863 principal will result in an extra $7,952 in interest and $10,863 in principal, or $18,815, that will be required to be paid during the life of the loan.

However, there are still some further limitations to this type of not-so-simple mortgage calculator, i.e., 1 ) no ability to adjust for the effects of present value and the time value of money. 

Step 5: Considering Present Value 

Let us now consider the present value or the time value of money. First, we will apply the current value to the results generated in Step 4. Click here to Compare the (Old) Mortgage To the (New) Mortgage Using Present Value. The default balances for the new and old loans are $100,000 and $102,000. The default "Mortgage Terms" for both loans is 30 years. The default rate for the new loan is 2.125%, and the default rate for the old one is 2.250%. 

However, there are two additional input fields: 1) an input field for a discount rate and 2) an input field for the costs of closing the loan. The discount rate field has a default value of 1.875%, and the "costs to close the loan" field has a default value of $2,500. For now, leave these set to their default values. 

Generating the results will show:

1. A difference in the rates of 0.125%.
2. A difference in the monthly payment of -$13.99.
3. There is a difference in total interest payments over the life of the two loans of $7,952.
4. A difference in total payments (principal & interest) over the life of the two loans of $18,815.
5. A present value of $404.
6. The cost to refinance is $2,500.
7. A net of -$2,096.

In determining a discount rate, we assume a flat yield curve. It would be much too complex to construct a yield curve using current treasury prices by applying a process called cubic splining and then subsequently discounting the difference in the cash flows between the two mortgages using the various rates along the curve to coincide with different cash flows. Therefore, it is deemed sufficient for consumers to assume a flat yield curve.